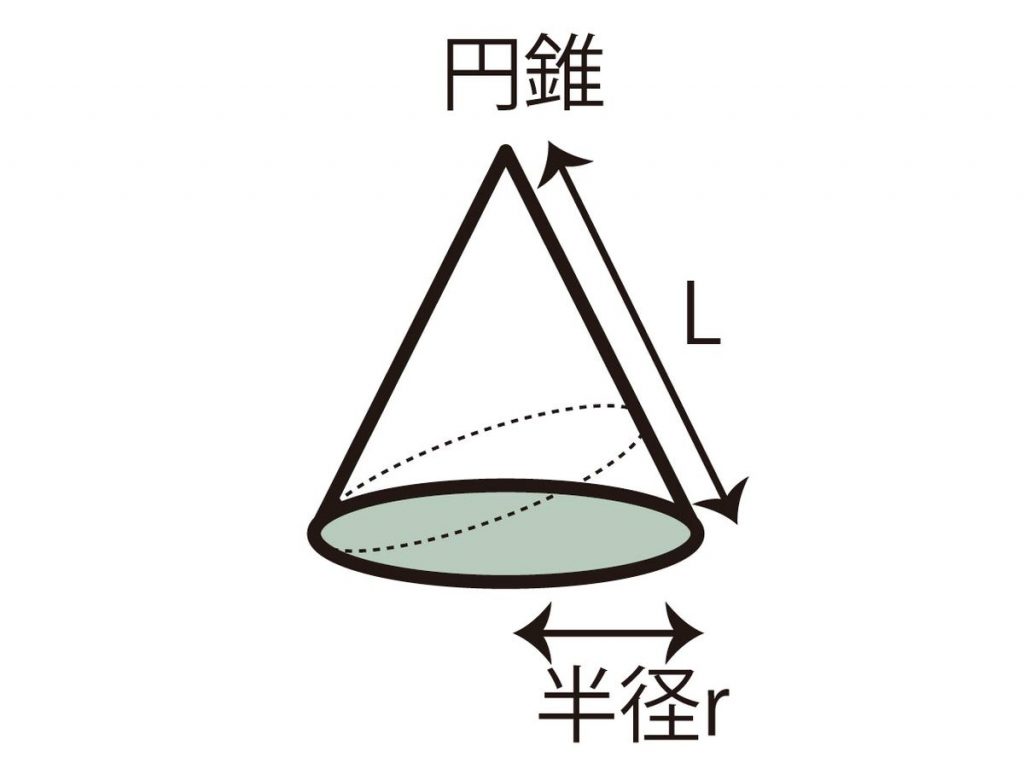
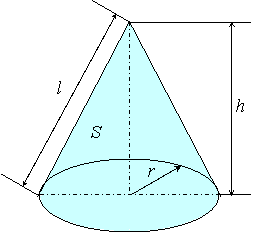
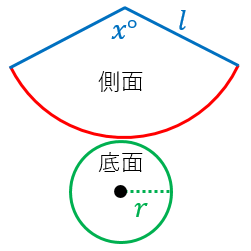
円錐の公式の導き方 円錐の展開図において, 側面のおうぎ形の半径 (円錐の母線)を, 側面のおうぎ形の弧の長さ (底面の円の周の長さ)を, おうぎ形の中心角を, 円錐の側面積 (おうぎ形の面積)を, 底面の円の半径を とする。 側面の扇形の弧の長さ 側面の扇形の面積 の式の両辺を2倍すると, を に分解して変形すると, 下線部は と同じ式であるから, これより,
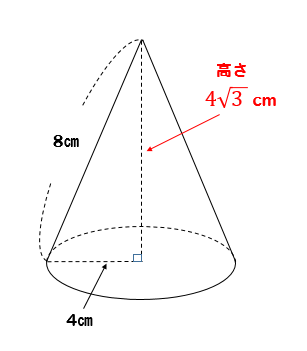
円錐 の 表面積 公式- 円錐は展開図にすると，円と扇形に分離されるのでこのような公式になります． 展開図がそのまま数式になっているので非常に分かりやすく理解しやすいと思います． 体積を求める公式 V = 1 3 π r 2 h V = 1 3 π r 2 h さて，次は円錐の体積を求める公式です 円錐の表面積の公式底面が半径rの円錐 図のような半径r の円を底面として母線がT の円錐の表面積S は$$\begin{eqnarray} S=\pi (rT)r \end{eqnarray}$$ と書けます。ただし, πは円周率を
円錐 の 表面積 公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「円錐 の 表面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「円錐 の 表面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「円錐 の 表面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「円錐 の 表面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「円錐 の 表面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  | |
「円錐 の 表面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「円錐 の 表面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「円錐 の 表面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |
角錐、円錐の体積 錐の体積 = 底面積 × 高さ× 1 3 高さとは>> 頂点から、底面におろした 垂線の長さのこと。 高さ (例) 底面 9cm 2 高さ 10cm 五角錐 体積=9×10÷3=30 正四角錐(底面が正方形) 4cm 6cm 高さ 底面積=4×4=16 体積=16×6÷3=32 高さ8cm 底面の半径 3cm 円錐 底面積=3×3×π=9π 体積=9π×8÷3=24π 例題 円すいの展開図、側面積の求め方！ 公式を使って15秒で解こう♪ 面積 面積 この円すいの側面積を求めなさい。 円周率は314とします。 知りたがり
Incoming Term: 円錐 の 面積 公式, 円錐 の 表面積 公式,
0 件のコメント:
コメントを投稿