2xy9x^2(2yx^21)\frac{dy}{dx}=0, y(0)=3 en Related Symbolab blog posts Advanced Math Solutions – Ordinary Differential Equations Calculator, Linear ODE Ordinary differential equations can be a little tricky In a previous post, we talked about a brief overview of This is a first order separable differential equation dy dx = y2 −4 dy y2 −4 = dx ∫ dy y2 − 4 = ∫dx Perform partial fraction 1 y2 −4 = A y 2 B y − 2 = A(y − 2) B(y 2) (y2 − 4) Compare the numerators 1 = A(y −2) B(y 2)F = x 2 y 4 x 2 y 4 ((x 2 y − 2 x y 2) d x (x 3 − 3 x 2 y) d y) = 0 Exact Differential Equation possible textbook mistake (3x^26xy^2) dx (6x^2y4y^2)dy = 0 and y(0)=2 Exact Differential Equation possible textbook mistake ( 3 x 2 6 x y 2 ) d x ( 6 x 2 y 4 y 2 ) d y = 0 and y ( 0 ) = 2

Engineering Mathematics Notes
(3y+4xy^(2))dx+(2x+3x^(2)y)dy=0
(3y+4xy^(2))dx+(2x+3x^(2)y)dy=0-Solution for (x^24*x*y2*y^2)dx (y^24*x*y2*x^2)dy=0 equation Simplifying (x 2 4x * y 2y 2) * dx (y 2 4x * y 2x 2) * dy = 0 Multiply x * y (x 2 4xy 2y 2) * dx (y 2 4x * y 2x 2) * dy = 0 Reorder the terms (4xy x 2 2y 2) * dx (y 2 4x * y 2x 2) * dy = 0 Reorder the terms for easier multiplication dx (4xy x 2 2y 2) (y 2 4x * y 2x 2) * dy = 0 (4xy * dx x 2 * dx 2y 2 * dx) (y 2 4x * y 2x 2) * dy = 0Solution for (x^2x*yy^2)dx (x*y)dy=0 equation Simplifying (x 2 1x * y y 2) * dx 1 (x * y) * dy = 0 Multiply x * y (x 2 1xy y 2) * dx 1 (x * y) * dy = 0 Reorder the terms (1xy x 2 y 2) * dx 1 (x * y) * dy = 0 Reorder the terms for easier multiplication dx (1xy x 2 y 2) 1 (x * y) * dy = 0 (1xy * dx x 2 * dx y 2 * dx) 1 (x * y) * dy = 0 Reorder the terms (dxy 2 1dx 2 y dx 3) 1 (x * y) * dy = 0 (dxy 2 1dx 2 y dx 3) 1 (x * y




Exercise 2 4 Marks Consider The Equation 2y 6x Dr 3r 4xy 1 Dy 0 1 Is It Exact 2 Use A Special Integrati Homeworklib
y = 2x^2c/x^2 > 2(y4x^2)dxxdy = 0 Which we can rearrange as follows dy/dx = (2 (y4x^2))/x " " = 8x(2y)/x dy/dx (2y)/x = 8xTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW `(3x yy^2)dx(x^2x y)dy=0` Solve (3x 2)2 d2y/dx2 3(3x 2)dy/dx 36y = 3x2 4x 1 Find the transformed equation of 4x^2 9y^2 – 8x 36y 4 = 0 when the axes are translated to the point (1, –2)
` (x^(2)y^(2)) dx 2xy dy = 0` Evaluate the following double integral $$ \int_{0}^{2}\int_{0}^{4x^2}\frac{xe^{2y}}{4y} \,dy\,dx $$ I am not sure how to proceed and our teacher mentioned something about changing the order of integration, but IAssuming y = 3^(4x) Take logs of both sides (you can use logs to any base but base e is a good idea as it has many applications in higher maths This is usually written as ln for natural log You should find it on your calculator together with log
Explanation We have (x −2y 1)dx (4x − 3y −6)dy = 0 Which we can write as dy dx = − x − 2y 1 4x −3y − 6 A Our standard toolkit for DE's cannot be used However we can perform a transformation to remove the constants from the linear numerator and denominator Consider the simultaneous equations 2 Answers2 There is no simple closed form for the solution, but one can find approximates Asymptotically, for x increasing y increases faster because y ′ ( x) > 2 Thus x y 2 → 0 1 y d y d x ≃ 2 → y ≃ e 2 x This is the first approximate More accurate approximates for low values of x can be derived on the form of series expansion$$5 x^{2} \frac{d}{d x} y{\left(x \right)} 4 x^{2} x y{\left(x \right)} \frac{d}{d x} y{\left(x \right)} 3 x y{\left(x \right)} y^{2}{\left(x \right)} = 0$$




Doc Differential Equations Tt Arafat Rahman Academia Edu




Engineering Mathematics Notes
Equations Tiger Algebra gives you not only the answers, but also the complete step by step method for solving your equations (2x^2y)dx(x^2yx)dy=0 so that you understand betterM(x,y)dx N(x,y)dy = 0 , with M(x,y) = 2xy , N(x,y) = y^3 4x^2 The equation is not exact because M_y = 2x # N_x = 8x Howevewer ( N_x M_y)/M = 5/y depends only on y and the integrating factor is IF = e^( lny^5) = 1/y^5 The new equation is P(x,y)dx Q(x,y)dy = 0 , with P(x,y) = 2x/y^4 , Q(x,y) = 1/y^2 4x^2/y^5ThisCombine all terms containing d \left (4y^ {2}x^ {2}3x4y\right)d=0 ( 4 y 2 x 2 − 3 x 4 y) d = 0 The equation is in standard form The equation is in standard form \left (4x^ {2}y^ {2}3x4y\right)d=0 ( 4 x 2 y 2 − 3 x 4 y) d = 0 Divide 0 by 3x4y4x^ {2}y^ {2} Divide 0 by − 3 x 4 y 4 x 2 y 2
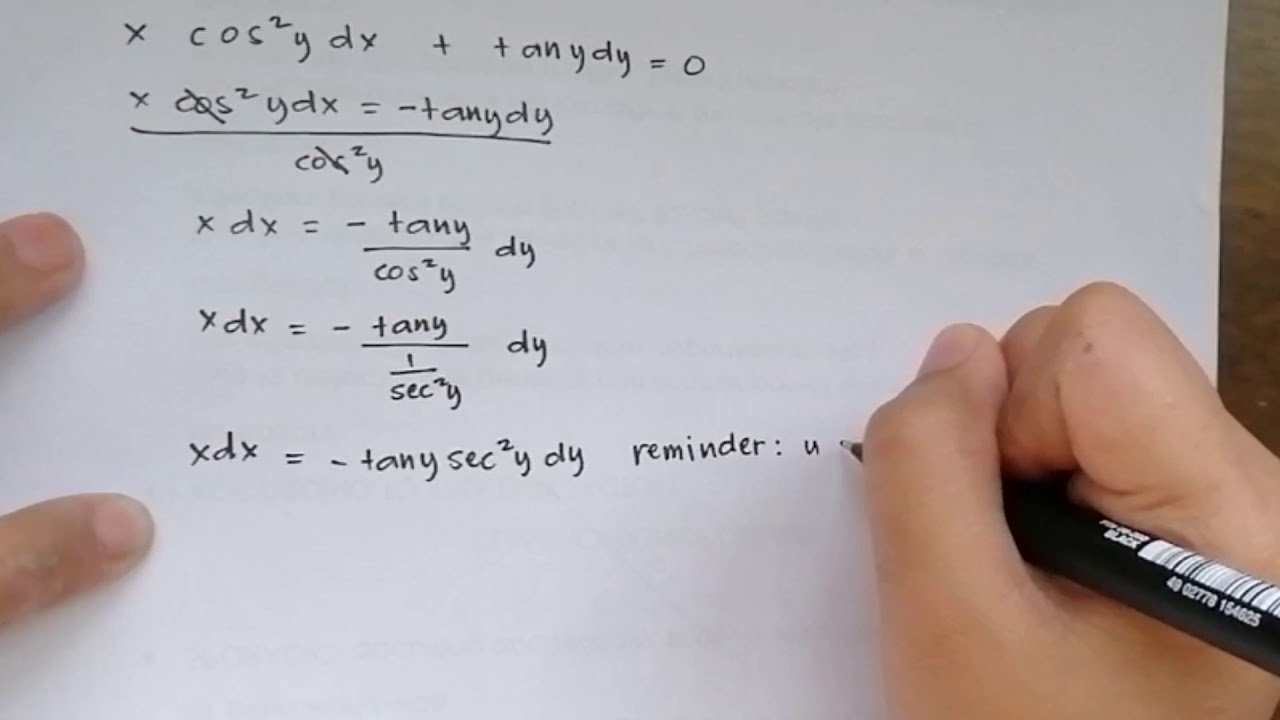



Xcos 2 Y Dx Tan Y Dy 0 Youtube




In Problems 31 Through 42 Verify That The Given Chegg Com
Solution for 4) (x – y)(4x y) dx x(5x – y) dy = 0 Q Given ω1= 32(cos 150° i sin cos 150°) ω2= 3(cos ° i sin cos °) Find the product of ω1 and ω2 A "Since you have posted a question with multiple subparts, we will solve the first three subparts for M = x 2 4xy 2y 2, N = y 2 4xy 2x 2 dM/dy = 4x 4y dN/dx = 4y 4x Therefore, dM/dy = dN/dx So, the given differential equation is exact On integrating M wrt x, treating y as a constant, On integrating N wrt y, treating x as a constant, (omitting 2xy 2 2x 2 y which already occur in ∫M dx) Therefore, the solution of` (1 x^(2)) (dy)/(dx) 2xy = 4x ^(2)`, given that `y = 0`, when `x =0` About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works




Solve Linear Differential Equation 4x 2y 6 Dx X 3dy 0 Brainly In




Solve The Differential Equation X Y 2 X Dx Y X 2 Y Dy 0
Txt 1609 hdrsgml 1609 accession number conformed submission type fwp public document count 8 filed as of date 1609 date as of change 1609 subject company company data company conformed name hsbc usa inc /md/ central index key Assuming you have an equation of the form M(x)dx N(y)dy = 0, if M y = N x, the equation is exact To solve, integrate M(x) with respect to x You should get a "constant" term that's actually a function of y alone, say g(y) Integrate N(y) with respect to y You should get another "constant" term that is a function of x alone, say f(x)4 y d x 2 y 2 d x (− 2 x 2 y d 2 y d) y = 0 Use the distributive property to multiply 2x^{2}yd2yd by y Use the distributive property to multiply − 2 x 2 y d 2 y d by y




Math 432 Hw 2 5 Solutions



Answered 1 Y 4x Y Dx 2 X Y Kdy 0 2 Bartleby
Given function is y = 4 4x 3/2 Now, differentiate the given function (4 4x 3/2) with respect to "x" dy/dx = d(4 4x 3/2)/dx dy/dx = 0 (3/2) × 4 × x 1/2 dy/dx = 6x (1/2) (1) To find arc length, we use the following formula for the length of the arc(L), L = \(\int_{a}^{b}\) √1 (dy/dx) 2 dxQuestion Dy/dx = 3x^2 = 4x 2/2(y 1) Seperate Variables Find General Solution This problem has been solved! The correct option (A) sin y = e x (x – 1)x –4 Explanation x 3 (dy/dx) 4x 2 tan y = e x secy Multiplying both sides by xcosy, ∴ x 4 cosy (dy/dx) 4x 3 siny = x ∙ e x ∴ (d/dx)(x 4 ∙ siny) = xe x ∴ x 4 ∙ siny = xe x – ∫e x dx c ∴ x 4 sin y = xe x – e x dx c (1) at x = 1, y = 0 ∴ sin 0



Answered N W Solve 1 Xdy 3ydx X Y Dx 2 Bartleby




Solve X Y 1 Dx 2x 2y 3 Dy 0 Youtube
$$4 x \frac{d}{d x} y{\left(x \right)} x 4 y{\left(x \right)} \frac{d}{d x} y{\left(x \right)} y{\left(x \right)} 10 \frac{d}{d x} y{\left(x \right)} 1 = 0$$Y' x^1 y = 4x^2y^1 cos x, x > 0 Dy/dx 1/2(tan x)y = 2y^3 sin x dy/dx 3/2x y = 6y^1/3 x^2 ln x y' 2x^1y = 6 squareroot 1 x^2 squareroot y, x > 0 Y' 2x^1y = 6y^2x^4 2x(y' y^3x^2) y = 0 (x a)(x b)(y' squareroot y) = 2(b a)y, where a, b are constants Y' 6x^1y = 3x^1y^2/3 cos x, x > 0 Y' 4xy = 4x^3y^1/2Calculus Find dy/dx y=3x^24x y = 3x2 − 4x y = 3 x 2 4 x Differentiate both sides of the equation d dx (y) = d dx (3x2 − 4x) d d x ( y) = d d x ( 3 x 2 4 x) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate the right side of the equation Tap for more steps



Solved Test Ii Solve The Equations Of Coefficients Linear In The Two Variables Y 2 Dx X Y 1 Dy 0 Course Hero




Y X 3 4x 2 5 Find Dy Dx D 2 Y Dx 2 And D 3 Y Dx 3
Write the equation as M(x,y)dx N(x,y)dy =0 with M = y(4x y 2 ) , M_y = 4x 2y 2 N = xy 1 , N_x = y # M_y Then the equation is not exact but (N_x M_y)/M = 1/y depends only on y The integrating factor is 1/y and leads to the equation P(x,y)dx N(x,y)dy =0 with P = 4x y 2 , P_yThe equation can be written as M(x,y)dx N(x,y)dy =0 with M = 6yx^2 4x , N = 2x^3 6y , M_y = N_x = 6x^2 The equation is exact ie is the total differential dF(x,y)=0 solved by F_x = M = 6yx^2 4x F_y = N = 2x^3 6y Integrating the firstSee the answer Show transcribed image text Expert Answer



What Is Ydx 2x Ye Y Dy 0 Quora



Http 1 160 97 198 8080 Xmlui Bitstream Handle 2 2 chapter 1 11 Pdf Sequence 2
Solution for y (4xy)dx2 (x^2y)dy=0 equation Simplifying y (4x y) * dx 2 (x 2 1y) * dy = 0 Reorder the terms for easier multiplication y * dx (4x y) 2 (x 2 1y) * dy = 0 Multiply y * dx dxy (4x y) 2 (x 2 1y) * dy = 0 (4x * dxy y * dxy) 2 (x 2 1y) * dy = 0 Reorder the terms (dxy 2 4dx 2 y) 2 (x 2 1y) * dy = 0 (dxy 2 4dx 2 y) 2 (x 2 1y) * dy = 0 Reorder the2xy9x^2(2yx^21)\frac{dy}{dx}=0, y(0)=3 es Related Symbolab blog posts Advanced Math Solutions – Ordinary Differential Equations Calculator, Linear ODE Ordinary differential equations can be a little tricky In a previous post, we talked about a brief overview of can you please explain how to to find dy/dx for the function x^2 y Y^2 x = 2 asked in CALCULUS by mathgirl Apprentice differentiation;




Math 432 Hw 2 5 Solutions Pdf Free Download




For Solving Dy Dx 4x Y 1 Suitable Substitution Is Youtube
Solution for (4xxy^2)dx(yx^2y)dy=0 equation Simplifying (4x xy 2) * dx (y x 2 y) * dy = 0 Reorder the terms for easier multiplication dx(4x xy 2) (y x 2 y) * dy = 0 (4x * dx xy 2 * dx) (y x 2 y) * dy = 0 (4dx 2 dx 2 y 2) (y x 2 y) * dy = 0 Reorder the terms 4dx 2 dx 2 y 2 (x 2 y y) * dy = 0 Reorder the terms for easier multiplication 4dx 2 dx 2 y 2 dy(x 2 y y) = 0 4dx 2 dx 2 y 2 (x 2 y * dy y * dy) = 0 4dx 2 dx 2 y 2 (dx 2 y 2 dy 2) = 0Steps for Solving Linear Equation ( x y ^ { 2 } x ) d x ( y x ^ { 2 } y ) d y = 0 ( x y 2 x) d x ( y x 2 y) d y = 0 Use the distributive property to multiply xy^ {2}x by d Use the distributive property to multiply x y 2 x by d \left (xy^ {2}dxd\right)x\left (yx^ {2}y\right)dy=0 A solution of the differential equation (dy/dx)2 – x(dy/dx) y = 0 is (A) y = 2 (B) y = 2x2 – 4 y = 2x (D) y = 2x – 4 Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries




Lista De Exercicos Equacoes Diferenciais Docsity



4xy 3y2 X Dx X X 2y Dy 0 Solve Non Exact Differential Equation By Inspection Method Brainly Ph
The integrating factor is 1/y^2 and leads to the equation P (x,y)dx Q (x,y)dy =0 , with P = 4x/y 1 , P_y = 4x/y^2 Q = 2/y 2x^2/y^2 , Q_x = P_y This equation is exact It is the total differential dF (x,y) =0 with solution F (x,y)=C obtained from F_x = P = 4x/y 1 F_y = Q = 2/y 2x^2/y^2 Substitute y = t x t ( t 2 x) = ( t − 2 x) y ′ Note that y ′ = t ′ x t t ( t 2 x) = ( t − 2 x) ( t ′ x t) After some simplifications you get t ′ ( t − 2 x) = 4 t Consider now x ′ = d x d t x ′ x 2 t = 1 4 Which is easy to solveSolve Y(4xy)dx 2(x^2y)dy = 0 By Finding The Integrating Factor And Test For Exactness Question Solve Y(4xy)dx 2(x^2y)dy = 0 By Finding The Integrating Factor And Test For Exactness This problem has been solved!




Practica 1 Ecuac Dif Analisis Matematico Ecuaciones



2
To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Solve `(xy^3y)dx2(x^2y^2xy^4)dy=0`Create your account View this answer (x23y2) dx−2xy dy = 0 ( x 2 3 y 2) d x − 2 x y d y = 0 ⇒ dy dxAnswer and Explanation 1 Become a Studycom member to unlock this answer!



Differential Equation Of Dy Dx 2x Y 4 4x 2y 1 Physics Forums




Pdf Lista De Exercicios De Equacoes Diferenciais Luis Fernando Fernandes De Olveira Academia Edu
Simple and best practice solution for (xy^24x)dx(yx^2y)dy=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve itStack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange(x2y2)dx=2xydy Geometric figure Two Straight Lines Slope = 1 xintercept = 0/1 = yintercept = 0/1 = Slope = 00/00 = 1000 xintercept = 0




Solucionarioecuacionesdiferencialesdenniszill7aedicion P




3y 2 X b Dx 2y Y 2 3 b Dy 0 Admits An Integrating Factor Which Is A Function Of X Y 2 Mathematics Stack Exchange




How To Do Implicit Differentiation 7 Steps With Pictures




2x 5y 3 Dx 2x 4y 6 Dy Mathematics Stack Exchange



Users Math Msu Edu Users Holmesir M2552 Hw2 Pdf
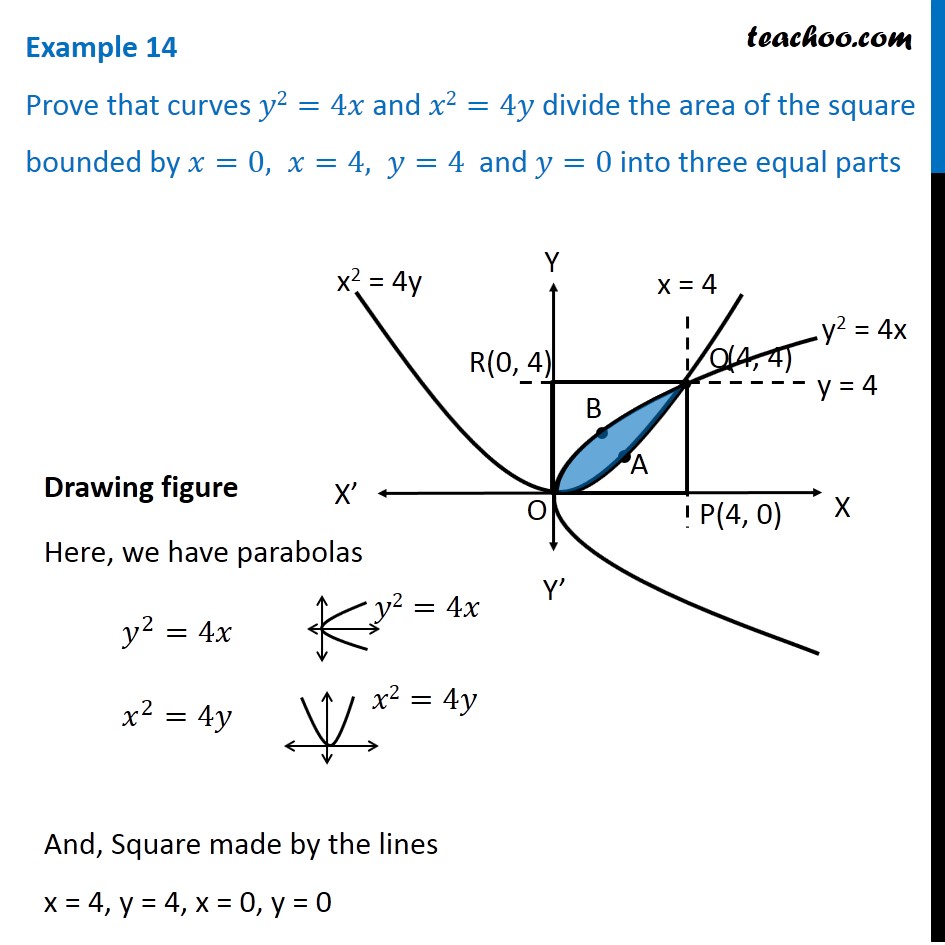



Example 14 Prove That Y2 4x X2 4y Divide Area Of Square




Ex 9 5 17 Mcq Which Is A Homogeneous Differential Equation



Http Www Math Sci Hokudai Ac Jp S Settepanella Teachingfile Calculus Calculus2 Pagine Lineintex Pdf




Solve This Plzzz 18 Find The Equations Of The Normal To The Curve Y 4x3 The Line 19 Maths Integrals Meritnation Com




Worked Example Identifying Separable Equations Video Khan Academy




1 Solve The Bvp 6xy 4 Dx 3x 2y Dy 0 Y 2 4 Chegg Com




Solve The Differential Equation Dy Dx Square 4x Y 1 Youtube



Solve The Differential Equations 2x Y 1 Dx 4x 2y 1 Dy 0 Sarthaks Econnect Largest Online Education Community



Q Tbn And9gcqqdjererih8cbajqv Puntih4ikbw7iy9bdv7cgyhxgixkwubp Usqp Cau



How To Solve The Differential Equation 2x 3y Dx 4x Y Dy 0 Quora




Verifying Solutions To Differential Equations Video Khan Academy




Engineering Mathematics Notes




Problem 4 Verify That The Differential Equation Is Exact Then Solve It 4x 2y Dx Homeworklib




Show That The Equation 5x4 3x2y2 2xy3 Dx 2x3y 3xy2 5y4 Dy 0 Is An Exact Differential Equation Find Its Solution Mathematics 2 Question Answer Collection
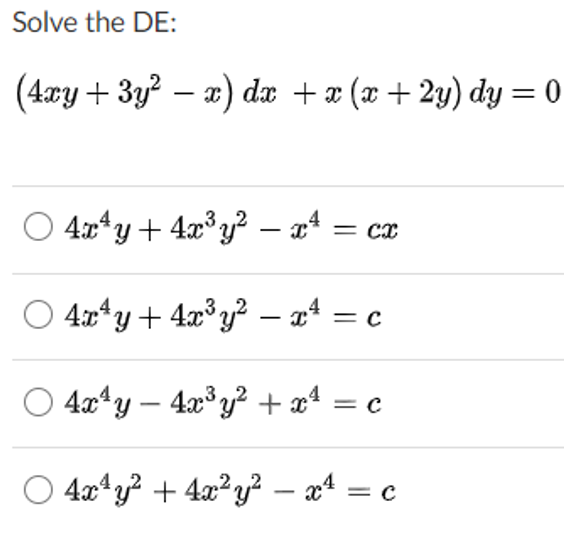



Answered Solve The De 4ry 3y X Dae X X Bartleby




Extra Questions Subtraction Elementary Mathematics




In Determine Whether The Given Differential Equation Chegg Com




Obtain The Particular Solution Satisfying The Initial Chegg Com




Solutions To Homework 2 Introduction To Differential Equations




Solve The Following X 2 4xy 2y 2 Dx Y 2 4xy 2x 2 Dy 0




Engineering Mathematics Notes




X2 Y2 Dx2xydy0 2dfracdydxdf See How To Solve It At Qanda



J5rlk8qlaoapwm



1 Y 4x Y Dx 2 X2 Y Dy 0 2 X 1 X 2 Chegg Com




How To Solve Exact Differential Equations In Matlab Stack Overflow




Obtain The Particular Solution Satisfying The Initial Chegg Com




4 Solve The Exact Differential Equation 1 2xy Dx 4y3 X2 Dy 0 4 Solve The Exact Differential Equation Homeworklib



Solve 3x 2 2 D 2y Dx 2 3 3x 2 Dy Dx 36y 3x 2 4x 1 Sarthaks Econnect Largest Online Education Community




Example 21 Find General Solution Ydx X 2y2 Dy 0



Solved Direction Give The General Solution Using Determination Of Integrating Factors X2 Y2 1 Dx X X 2y Dy 0 2 Y 4x Y Dx 2 X2 Course Hero




Tentukan Solusi Dari 3x 4xy Dx 2x 3y Dy 0 Brainly Co Id



How To Solve Dy Dx Y 4x 2 Quora
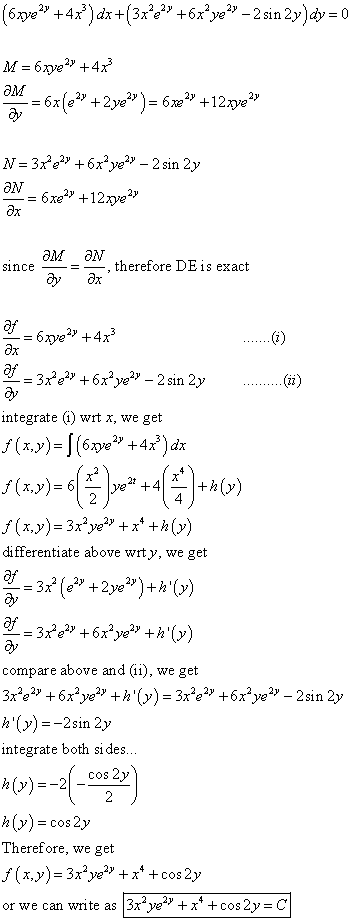



Differential Equations Solved Examples 17



2
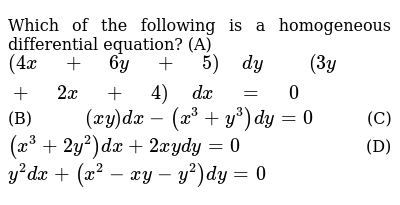



Which Of The Following Is A Homogeneous Differential Equation A 4x 6y 5 Dy 3y 2x 4 Dx 0 B X Y Dx X 3 Y 3 Dy 0 C X 3 2y 2 Dx 2x Ydy 0 D Y 2dx X 2 X Y Y 2 Dy 0




3y 2 X b Dx 2y Y 2 3 b Dy 0 Admits An Integrating Factor Which Is A Function Of X Y 2 Mathematics Stack Exchange




Ecuaciones Diferenciales Exactas Canek Uam




Engineering Mathematics Notes




Solucionarioecuacionesdiferencialesdenniszill7aedicion P




Solution Of X 2 4xy 2y 2 Dx Y 2 4xy 2x 2 Dy 0 Is




If X2 Y2 2 Xy Find Dy Dx Mention Each And Every Step Mathematics Topperlearning Com Gwvwfskk




Solve The Following Differential Equations A Xdy Y Dx I X Dx Y Dy 2




Exercises Solve Each Of The Differential Equations In Chegg Com



The Solution Of Y 2x 2y E X Dx E X Y 3 Dy 0 If Y 0 1 Is Sarthaks Econnect Largest Online Education Community




Differential Equations



Is 1 3 X Sin Y Dx X2 Cos Y Dy 0 Quora



Find The Particular Solution Of The Differential Equation 3xy Y 2 Dx X 2 Xy Dy 0 For X 1 Y 1 Sarthaks Econnect Largest Online Education Community
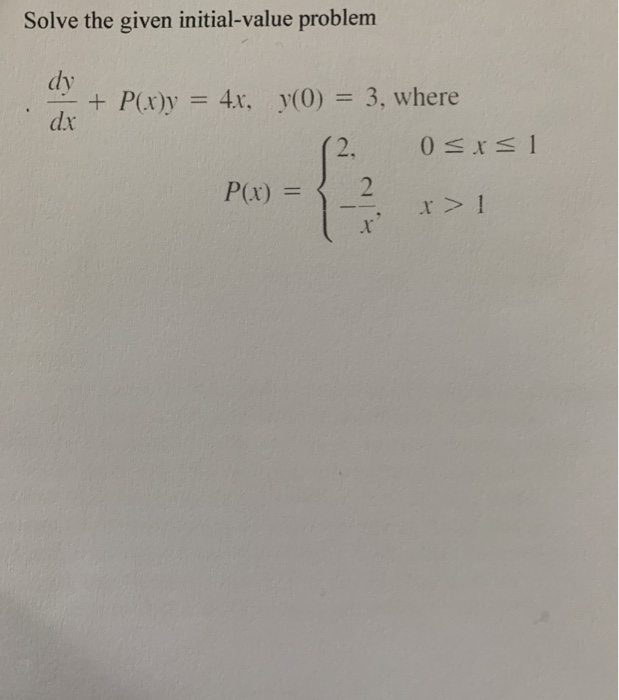



Solve The Given Initial Value Problem Dy Dx P X Y 4x Y 0 4x Y 0 3 Where 2 0 Wegglab




Solucionarioecuacionesdiferencialesdenniszill7aedicion P




Engineering Mathematics Notes




What Is The Solution To This Ode 3x 2 4xy Y 2 Dx 2x 2 2xy 9 Dy 0 Quora



Q Tbn And9gct Hzrurro7l4jfiofq3eyyanghflf8gqycicnedos0inaplml9 Usqp Cau



How To Solve 4y X 2y Dy 2x Xy 2 Dx 0 Quora




How To Do Implicit Differentiation 7 Steps With Pictures



Dy Dx 4x Y 1 2 Youtube



What Is The General Solution Of 2y X Dx Y 2x Dy 0 Quora



2ye Dy V E 2x Cos Xº Dx Y 4x Y Dx Chegg Com
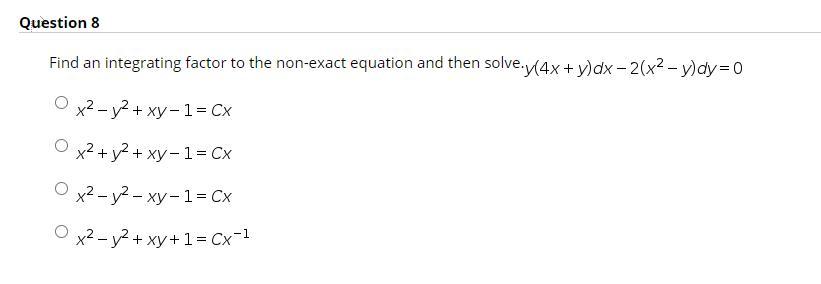



Solved Question 8 Find An Integrating Factor To The Non E Chegg Com



Find Dy Dx Of X 2 Y 2 2 4xy Sarthaks Econnect Largest Online Education Community




Ecuaciones Diferenciales Guia N 2




Pdf 2 6 Exact Differential Equations And Integrating Factors Mirna Mansour Academia Edu



7x 3y 1 0



Solved Y 4x Y Dx 2 X 2 Y Dy 0 Solve This Give Me Explanation And Clear Writings Course Hero



Www Tau Ac Il Levant Ode Solution 6 Pdf




Mth 311 Lecture 3 Ch2 Intro To Diff Eq S Continued Oneclass




Math 432 Hw 2 4 Solutions Frostburg




Math 432 Hw 2 5 Solutions Frostburg
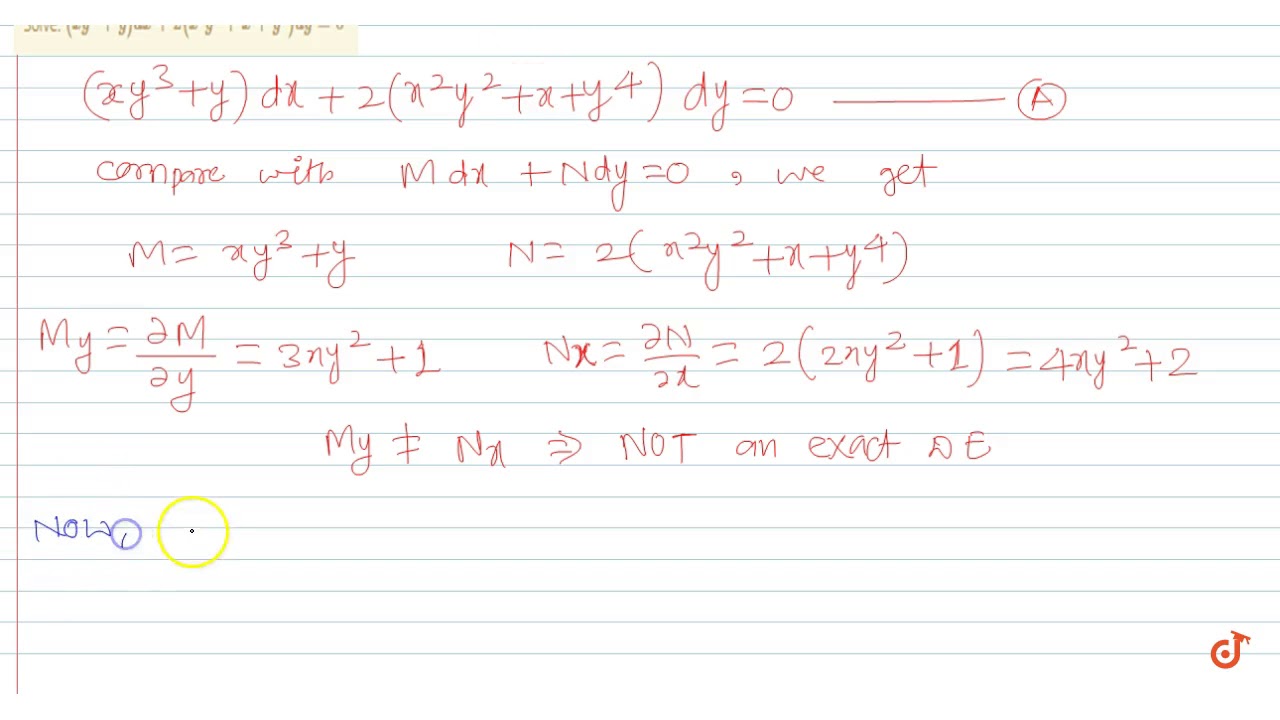



Solve Xy 3 Y Dx 2 X 2y 2 X Y 4 Dy 0 Youtube
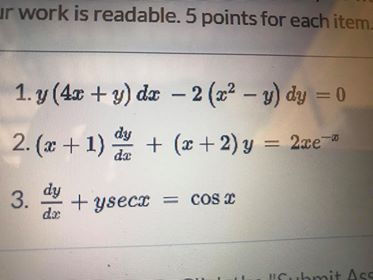



Ur Work Is Readable 5 Points For Each Item 1 Y 4x Chegg Com



1




If Y E 4x Sin 3x Find D 2 Y Dx 2




Exercise 2 4 Marks Consider The Equation 2y 6x Dr 3r 4xy 1 Dy 0 1 Is It Exact 2 Use A Special Integrati Homeworklib




Ex 9 5 4 Show Homogeneous X2 Y2 Dx 2xy Dy 0 Ex 9 5




Answered 4x Y Dx X Y X Dy 0 An Bartleby




Differential Equatio Long Answer Questions 7 M R Solye 2x Y 3 Dx 2y X 1 Dy Sol Dy 2x Y 3 Given Equation Is
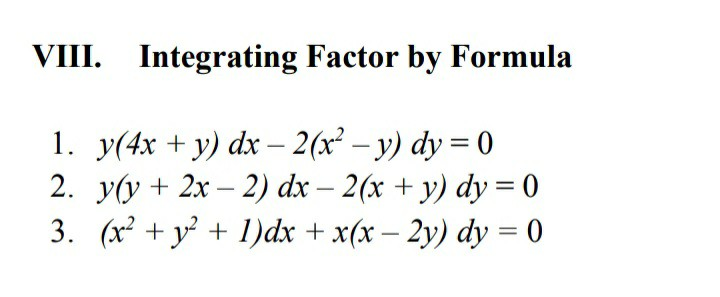



Viii Integrating Factor By Formula 1 Y 4x Y Dx Chegg Com



Q Tbn And9gcq69xqaiwgxy95 44f5sqsm2pnlgxvor Roue6xadfczqpkv4qx Usqp Cau



0 件のコメント:
コメントを投稿